ML a neurónové siete v praktických príkladoch / 1 časť: Teoretické minimum

Základy ML a neurónových sietí na praktických príkladoch

 

I. Na úvod trochu zrozumiteľnej teórie

Začneme vysvetlením rozdielu medzi strojovým učením a klasickým programovaním. Pri klasickom programovaní je naším cieľom vymyslieť a implementovať algoritmus, ktorý spracuje vstupné údaje tak, aby sa dosiahol požadovaný výsledok. Pri učení neurónových sietí máme k dispozícii veľké množstvo množín vstupných údajov a k nim známe prislúchajúce výsledky a naším cieľom je, aby si model neurónovej siete vytvoril čo najpresnejší algoritmus, ktorý zo vstupných údajov vytvorí požadované výstupy. Model natrénovaný na známych prípadoch sa následne využije na generovanie výstupov pre ďalšie množiny vstupov, pre ktoré nepoznáme výsledky. Typický príklad je predpovedanie, či klient banky bude splácať úver. Model bol natrénovaný na veľkom množstve doterajších prípadov, pri ktorých vieme, ako to dopadlo. Na základe vstupných atribútov, v tomto prípade je to vek, pohlavie, povolanie, rodinný stav, počet detí, región a mnoho ďalších údajov, ktoré banka od žiadateľa o úver vyžaduje, model vygeneruje výstup – pravdepodobnosť, s akou klient úver splatí.

Deep learning

Deep learning čiže hlboké strojové učenie je metóda strojového učenia, kde algoritmus pomocou mnohovrstvových nelineárnych výpočtových modelov dokáže z údajov získať informácie. Modely deep learning využívajú neurónové siete s veľkým množstvom vrstiev. Aj jednoduché modely majú väčšinou najmenej desať vrstiev, komplexnejšie aj stovky či tisícky vrstiev. Modely sa trénujú na obrovskom množstve údajov. Čím väčšie je množstvo tréningových dát, tým presnejšie výsledky daný model pri predikciách dosahuje. Trénovanie je časovo náročné, natrénovaný model potom možno použiť na predikcie v reálnom čase.

Trénovanie neurónovej siete

Algoritmus trénovania funguje v slučke, ktorá má v každom cykle dve fázy:

• dopredný prechod (Forward propagation)
• spätný prechod (Back propagation)

 Na začiatku trénovania sa inicializujú váhové koeficienty všetkých neurónov. Spravidla sa na inicializáciu použijú náhodné hodnoty. Pri doprednom prechode sa vypočíta chyba čiže odchýlka predikovanej hodnoty od skutočnej. Následne sa v spätnom prechode slučkou váhové koeficienty upravujú tak, aby sa táto chyba minimalizovala. Tento postup predného a spätného prechodu sa neustále opakuje dovtedy, pokiaľ sa nedosiahne minimálna hodnota chyby.

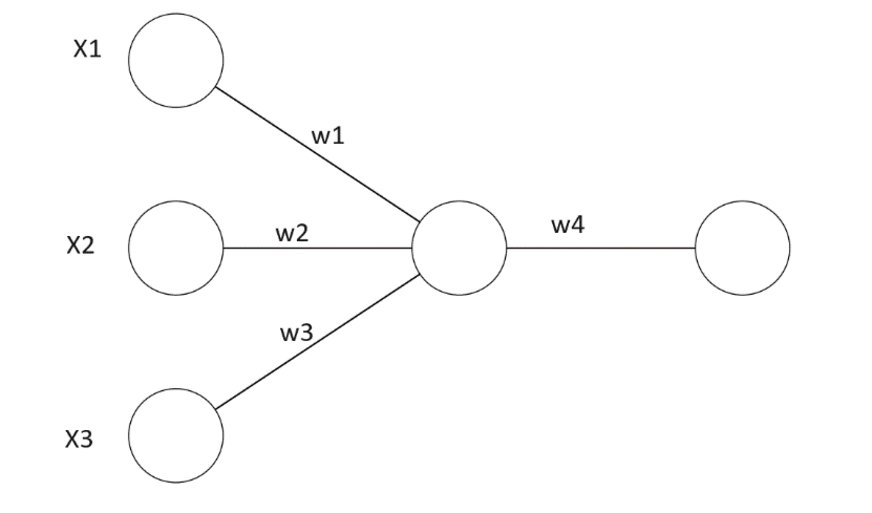
Princípy budeme vysvetľovať na neurónovej sieti, ktorá má tri vstupy x1, x2 a x3, jeden neurón v skrytej vrstve a jeden neurón vo výstupnej vrstve. Hodnoty w1, w2 a w3 sú váhové koeficienty jednotlivých vstupov a w4 je váhový koeficient výstupu neurónu v skrytej vrstve.

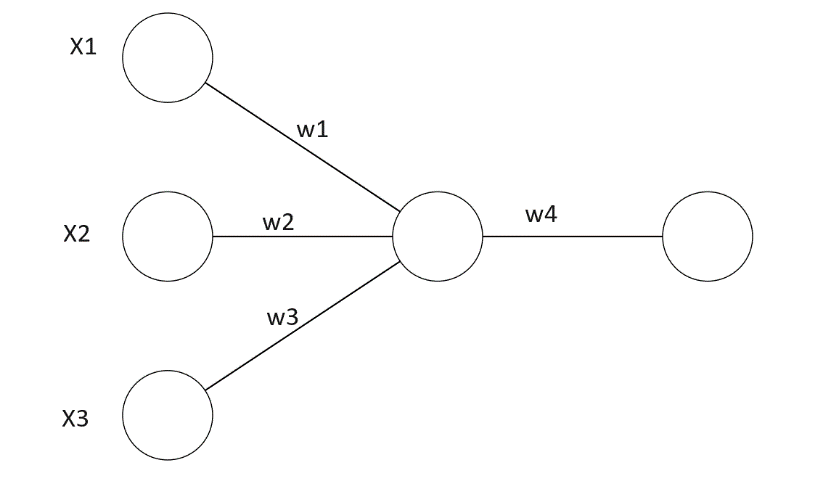
Definujeme stratovú funkciu, nazývanú aj chybová funkcia, čo je rozdiel medzi očakávaným výstupom y a aktuálnym výstupom y^. Pre túto funkciu sa často využíva označenie loss, my ju pre jednoduchosť budeme označovať písmenom e (error).

e = (y - y ^)

Hlavným cieľom pri trénovaní neurónových sietí je čo najviac znížiť túto chybu.

Derivácie

V tomto ohľade máme dve správy, dobrú a zlú. Zlá správa je, že pri vysvetľovaní dopredného a spätného prechodu a ďalších funkcií súvisiacich s modelmi neurónových sietí sa nezaobídeme bez derivácií, takže by bolo dobré vedieť, čo to derivácia je a aký má matematický a geometrický význam. Dobrá správa je, že derivácie nebudete musieť ani počítať, ani programovať, knižnice typu PyTorch, Keras či TensorFlow to zvládnu samy.

Derivácia funkcie je zmena tejto funkcie v pomere k veľmi malej zmene jej premennej či premenných. Opačným procesom k derivovaniu je integrovanie. V prípade dvojrozmerného grafu funkcie f(x) je derivácia tejto funkcie v ľubovoľnom bode rovná smernici dotyčnice tohto grafu.

Pre zmenu hodnoty sa používa symbol Δ, takže tento pomer možno symbolicky zapísať ako:

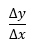
Derivácia je hodnota podielu pre Δx blížiacej sa k 0. Ak nahradíme konečne malý rozdiel Δx nekonečne malou zmenou dx, získame definíciu derivácie:

 

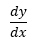
Dopredné šírenie (Forward Propagation)

Prvý krok je v dopredné šírenie, keď sa na vstupy aplikujú váhové koeficienty, zjednodušene váhy, v našom prípade w1, w2 a w3.

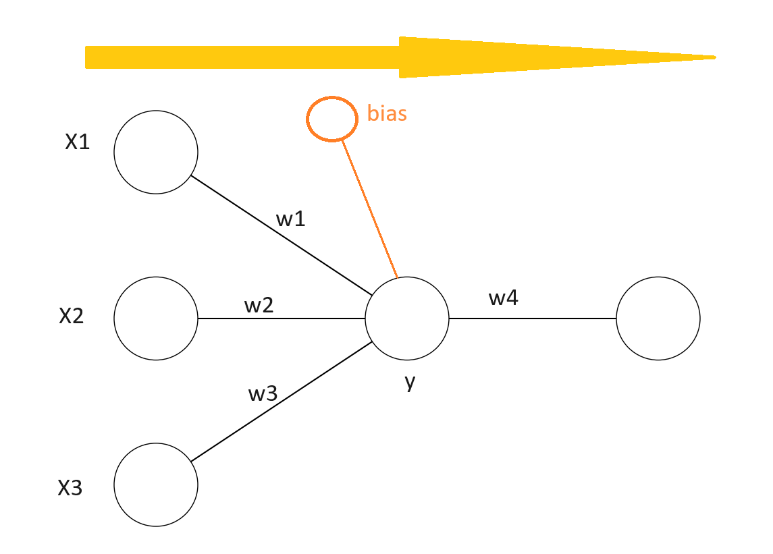
Na začiatku trénovania sú tieto váhové koeficienty priradené náhodne. Výstupom každého neurónu je súčet súčinov vstupov a im priradených váhových koeficientov. K súčtu pripočítame aj bias.

Výstup z prvej vrstvy teda bude:

y = (w1x1 + w2x2 + w3x3) + bias

Na vypočítanú hodnotu potom aplikujeme vhodnú aktivačnú funkciu. Pri nelineárnych úlohách sa vyžaduje nelineárna aktivačná funkcia. Aktivačné funkcie budú vysvetlené v samostatnej stati.

Keď vypočítame výstup y ^, následne vypočítame stratovú funkciu, ktorá udáva, ako veľmi je vypočítaný výstup nepresný. Našíim cieľom je túto nepresnosť minimalizovať. Dosiahneme to aktualizáciou váhových koeficientov.

Spätné šírenie (back propagation)

Váhové koeficienty sa budú aktualizovať počas spätného prechodu. Odvodíme a vysvetlíme vzorec na aktualizáciu váhových koeficientov.

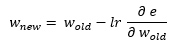
Kde

lr – rýchlosť učenia (learning rate)

e – stratová funkcia (loss)

Tento vzorec využíva reťazové pravidlo diferenciácie.

Keďže derivácia 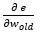 udáva sklon dotyčnice, parciálna derivácia  udáva sklon dotyčnice krivky gradientného zostupu (gradient descent). Je to krivka, kde na osi x je príslušný váhový koeficient a na osi y aktuálna hodnota chyby.

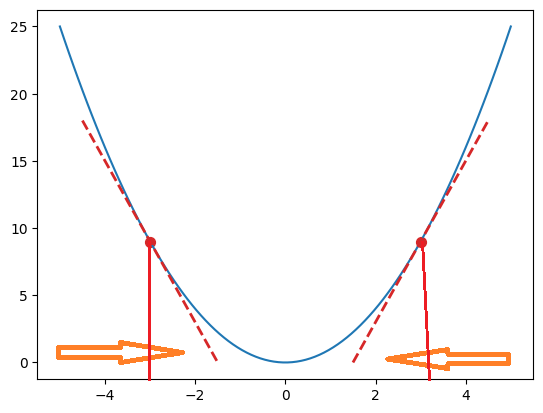
Naším cieľom je nájsť bod najmenšej chyby čiže lokálne minimum. V procese trénovania preto priebežne aktualizujeme váhové koeficienty. Sklon vľavo je zostupný alebo záporný a naznačuje, že hodnotu váhového koeficientu treba zvýšiť. Sklon vpravo je vzostupný alebo kladný a hodnotu váhového koeficientu je potrebné v takomto prípade znížiť. Mieru zníženia alebo zvýšenia určuje koeficient udávajúci rýchlosť učenia. Spravidla je to malé číslo, napríklad 0,01. Tento proces sa v jednotlivých cykloch opakuje dovtedy, kým sa nedosiahne minimum. Vtedy bude dotyčnica rovnobežná s osou x.

V budúcom pokračovaní vysvetlíme optimalizačný algoritmus zostup gradientu (gradient descent), ktorý sa využíva na trénovanie modelov strojového učenia a neurónových sietí, a predstavíme najpoužívanejšie aktivačné funkcie.

Zobrazit Galériu